All About Mathematics

DEFINITION OF MATHEMATICS: The study of the measurement, properties, and relationships of quantities and sets, using numbers and symbols.  absolute value The distance of a number from zero; the positive value of a number.  acute angle A positive angle measuring less than 90 degrees.  Understanding math concepts is critical in our world today. Math is used daily by nearly everyone, from lay persons to highly degreed professionals. Situations in which math is used vary from simply balancing a checkbook or calculating the amount of change due from a store transaction all the way to making blueprints for an office building or house and the construction of those buildings. Understanding how to solve math problems becomes easier as one learns math terminology. Below is a list of many common math terms and their definitions. Acute angle – An angle which measures below 90°. Acute triangle – A triangle containing only acute angles. Additive inverse – The opposite of a number or its negative. A number plus its additive inverse equals 0. Adjacent angles – Angles with a common side and vertex. Angle – Created by two rays and containing an endpoint in common. Arc – A set of points that lie on a circle and that are positioned within a central angle. Area – The space contained within a shape. Average – The numerical result of dividing the sum of two or more quantities by the number of quantities. Binomial – An expression in algebra that consists of two terms. Bisect – To divide into two equal sections. Canceling – In multiplication of fractions, when one number is divided into both a numerator and a denominator. Cartesian coordinates – Ordered number pairs that are assigned to points on a plane. Chord – A line segment that connects two points on a circle. Circle – A set of points that are all the same distance from a given point. Circumference – The distance measured around a circle. Coefficient – A number that is placed in front of a variable. For example, in 6x, 6 is the coefficient. Common denominator – A number that can be divided evenly by all denominators in the problem. Complementary angles – Two angles in which the sum of their measurements equals 90°. Complex fraction – A fraction that contains a fraction or fractions in the numerator and/or denominator. Congruent – Exactly the same. Identical in regard to size and shape. Coordinate graph – Two perpendicular number lines, the x axis and the y axis, which make a plane upon which each point is assigned a pair of numbers. Cube – A solid with six sides, with the sides being equal squares and the edges being equal. Also, the resulting number when a number is multiplied by itself twice. Cube root – A number that when multiplied by itself twice gives the original number. For example, 4 is the cube root of 64. Decimal fraction – Fraction with a denominator of 10, 100, 1,000, etc., written using a decimal point. Degree – The measurement unit of an angle. Denominator – The bottom symbol or number of a fraction. Diameter – A line segment that contains the center and has its endpoints on the circle. Also, the length of this segment. Difference – That which results from subtraction. Equation – A relationship between symbols and/or numbers that is balanced. Equilateral triangle – A triangle that has three equal angles and three sides the same length. Even number – An integer which can be divided by 2, with no remainder. Expanded notation – To point out the place value of a digit by writing the number as the digit times its place value. Exponent – A positive or negative number that expresses the power to which the quantity is to be raised or lowered. It is placed above and to the right of the number. Exterior angle – In a triangle, an exterior angle is equal to the measures of the two interior angles added together. Factor – As a noun, it is a number or symbol which divides evenly into a larger number. As a verb, it means to find two or more values whose product equals the original value. F.O.I.L. Method – A method used for multiplying binomials in which the first terms, the outside terms, the inside terms, and then the last terms are multiplied. Fraction – A symbol which expresses part of a whole. It contains a numerator and a denominator. Greatest common factor – The largest factor that is common to two or more numbers. Hypotenuse – In a right triangle it is the side opposite from the 90° angle. Imaginary number – The square root of a negative number. Improper fraction – A fraction in which the numerator is larger than the denominator. Integer – A whole number. It may be positive, negative, or zero. Interior angles – Angles formed inside the shape or inside two parallel lines. Intersecting lines – Lines that come together at a point. Interval – The numbers that are contained within two specific boundaries. Irrational number – A number that is not rational (cannot be written as a fraction x/y, with x a natural number and y an integer). Isosceles triangle – A triangle with two equal sides and two equal angles across from them. Least common multiple – The smallest multiple that is common to two or more numbers. Linear equation – An equation where the solution set forms a straight line when it is plotted on a coordinate graph. Lowest common denominator – The smallest number that can be divided evenly by all denominators in the problem. Mean – The average of a number of items in a group (total the items and divide by the number of items). Median – The middle item in an ordered group. If the group has an even number of items, the median is the average of the two middle terms. Mixed number – A number containing both a whole number and a fraction. Monomial – An expression in algebra that consists of only one term. Natural number – A counting number. Negative number – A number less than zero. Nonlinear equation – An equation where the solution set does not form a straight line when it is plotted on a coordinate graph. Number line – A visual representation of the positive and negative numbers and zero. Numerator – The top symbol or number of a fraction. Obtuse angle – An angle which is larger than 90° but less than 180°. Obtuse triangle – A triangle which contains an obtuse angle. Odd number – An integer (whole number) that is not divisible evenly by 2. Ordered pair – Any pair of elements (x,y) where the first element is x and the second element is y. These are used to identify or plot points on coordinate graphs. Origin – The intersection point of the two number lines of a coordinate graph. The intersection point is represented by the coordinates (0,0). Parallel lines – Two or more lines which are always the same distance apart. They never meet. Percentage – A common fraction with 100 as its denominator. Perpendicular lines – Two lines which intersect at right angles. Pi (π) – A constant that is used for determining the circumference or area of a circle. It is equal to approximately 3.14. Polynomial – An expression in algebra that consists of two or more terms. Positive number – A number greater than zero. Power – A product of equal factors. 3 x 3 x 3 = 33, read as “three to the third power” or “the third power of three.” Power and exponent can be used interchangeably. Prime number – A number that can be divided by only itself and one. Proper fraction – A fraction in which the numerator is less than the denominator. Proportion – Written as two equal ratios. For example, 5 is to 4 as 10 is to 8, or 5/4 = 10/8. Pythagorean theorem – A theorem concerning right triangles. It states that the sum of the squares of a right triangle’s two legs is equal to the square of the hypotenuse (a2 + b2 = c2). Quadrants – The four divisions on a coordinate graph. Quadratic equation – An equation that may be expressed as Ax2 + Bx + C = 0. Radical sign – A symbol that designates a square root. Radius – A line segment where the endpoints lie one at the center of a circle and one on the circle. The term also refers to the length of this segment. Ratio – A comparison between two numbers or symbols. May be written x:y, x/y, or x is to y. Rational number – An integer or fraction such as 7/7 or 9/4 or 5/1. Any number that can be written as a fraction x/y with x a natural number and y an integer. Reciprocal – The multiplicative inverse of a number. For example, 2/3 is the reciprocal of 3/2. Reducing – Changing a fraction into its lowest terms. For example, 3/6 is reduced to ½. Right angle – An angle which measures 90°. Right triangle – A triangle which contains a 90° angle. Scalene triangle – A triangle in which none of the sides or angles are equal. Scientific notation – A number between 1 and 10 and multiplied by a power of 10. Used for writing very large or very small numbers. Set – A group of objects, numbers, etc. Simplify – To combine terms into fewer terms. Solution, or Solution set – The entirety of answers that may satisfy the equation. Square – The resulting number when a number is multiplied by itself. Also, a four-sided figure with equal sides and four right angles. The opposite sides are parallel. Square root – The number which when multiplied by itself gives you the original number. For example, 6 is the square root of 36. Straight angle – An angle which is equal to 180°. Straight line – The shortest distance between two points. It continues indefinitely in both directions. Supplementary angles – Two angles that when combined the sum equals 180°. Term – A literal or numerical expression that has its own sign. Transversal – A line which crosses two or more parallel or nonparallel lines in a plane. Triangle – A three-sided closed figure. It contains three angles that when combined the sum equals 180°. Trinomial – An expression in algebra which consists of three terms. Unknown – A symbol or letter whose value is unknown. Variable – A symbol that stands for a number. Vertical angles – The opposite angles that are formed by the intersection of two lines. Vertical angles are equal. Volume – The amount which can be held, as measured in cubic units. The volume of a rectangular prism = length times width times height. Whole number – 0, 1, 2, 3, 4, 5, 6, 7, 8, etc. X-axis – The horizontal axis on a coordinate graph. X-coordinate – The first number in an ordered pair. It refers to the distance on the x-axis. Y-axis – The vertical axis on a coordinate graph. Y-coordinate – The second number in an ordered pair. It refers to the distance on the y-axis. Algebra Formulas Here are some of the most commonly used formulas in algebra. If you have one you'd like to be added, or find an error, please contact me. Laws of Exponents (am)(an) = am+n (ab)m = ambm (am)n = amn a0 = 1 (am)/(an) = am-n a-m= 1/(am) Quadratic Formula In an equation like ax2 + bx + c = 0 You can solve for x using the Quadratic Formula: Binomial Theorem (a + b)1 = a + b (a + b)2 = a2 + 2ab + b2 (a + b)3 = a3 + 3a2b + 3ab2 + b3 (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 ...and so on... Difference of Squares a2 - b2 = (a - b)(a + b) Rules of Zero 0/x = 0 where x is not equal to 0. a0 = 1 0a = 0 a*0 = 0 a/0 is undefined (you can't do it) Basic math formulas  Average formula: Let a1,a2,a3,......,an be a set of numbers, average = (a1 + a2 + a3,+......+ an)/n Fractions formulas: Converting a mixed number to an improper fraction: Converting an improper fraction to a mixed number: Formula for a proportion: In a proportion, the product of the extremes (ad) equal the product of the means(bc), Thus, ad = bc Percent: Percent to fraction: x% = x/100 Percentage formula: Rate/100 = Percentage/base Rate: The percent. Base: The amount you are taking the percent of. Percentage: The answer obtained by multiplying the base by the rate Consumer math formulas: Discount = list price × discount rate Sale price = list price − discount Discount rate = discount ÷ list price Sales tax = price of item × tax rate Interest = principal × rate of interest × time Tips = cost of meals × tip rate Commission = cost of service × commission rate Geometry formulas: Perimeter: Perimeter of a square: s + s + s + s s:length of one side Perimeter of a rectangle: l + w + l + w l: length w: width Perimeter of a triangle: a + b + c a, b, and c: lengths of the 3 sides Area: Area of a square: s × s s: length of one side Area of a rectangle: l × w l: length w: width Area of a triangle: (b × h)/2 b: length of base h: length of height Area of a trapezoid: (b1 + b2) × h/2 b1 and b2: parallel sides or the bases h: length of height volume: Volume of a cube: s × s × s s: length of one side Volume of a box: l × w × h l: length w: width h: height Volume of a sphere: (4/3) × pi × r3 pi: 3.14 r: radius of sphere Volume of a triangular prism: area of triangle × Height = (1/2 base × height) × Height base: length of the base of the triangle height: height of the triangle Height: height of the triangular prism Volume of a cylinder:pi × r2 × Height pi: 3.14 r: radius of the circle of the base Height: height of the cylinder Have any questions about the basic math formulas? Send me an email here and ask me any questions you want about these basic math formulas   What are Illustrations of  formulas? Formulas are statements of algebra, which apply to numbers of a definition set. They can be proved except the axioms. You can deduce new formulas by well-known formulas by logical reasoning. This procedure is called a proof. The proof  ideas and also the proof ways can be described by pictures. In addition the formulas themselves become more alive. 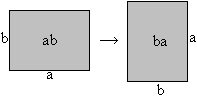You can find illustrations of well known formulas on this page. Simple Formulas  top Commutative law of multiplication (Axiom) ab=ba 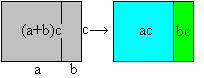Distributive law (Axiom) (a+b)c=ac+bc Product of a difference and a number 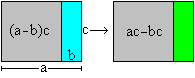(a-b)c=ac-bc Product of two sums 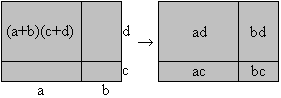(a+b)(c+d)=ac+ad+bc+bd Product of two differences 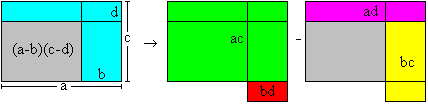(a-b)(c-d)=  ac+bd  -ad-bc Product of a sum and a difference 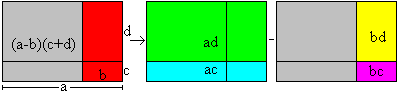(a-b)(c+d)=  ac+ad   -bc-bd Looking for a parallelogram with the same area 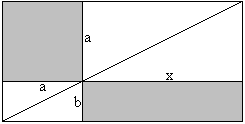a²=bx Binomial Formulas   top 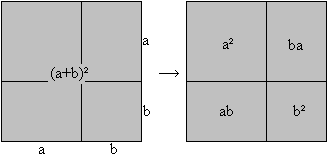First binomial formula (a+b)²=a² + 2ab + b²  Second binomial formula (a-b)²=  b²+a²  -2ab Third binomial formula 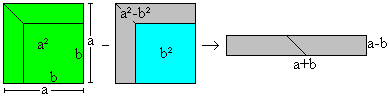a²-b²=(a+b)(a-b) Tri-nomial formula 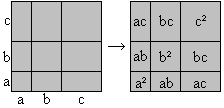(a+b+c)²=a²+b²+c²+2ab+2ac+2bc Difference of the squares of a sum and a difference 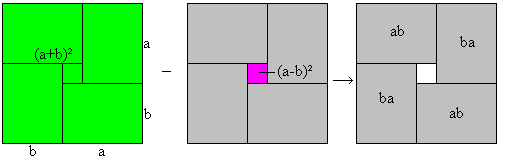(a+b)²-(a-b)²=4ab Pythagoras's Theorem  top 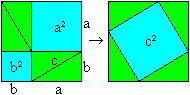The Pythagorean theorem (Pythagoras or one of his students, Pythagoras of Samos, 580-500 BC) a²+b²=c² The Pythagorean theorem (Euklid, ~300 BC)  Classical proof with triangles 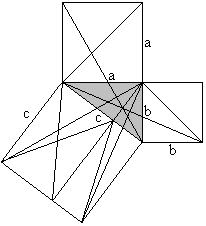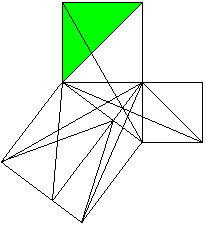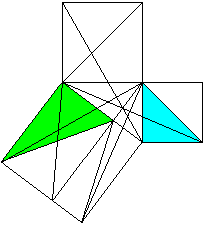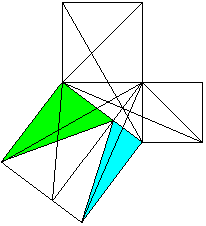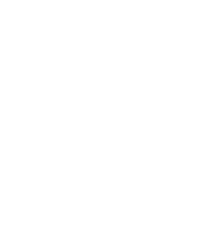a²+b²=c²  The Pythagorean theorem (Euklid, ~300 BC) Proof with four-sided figures 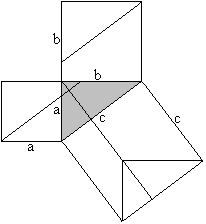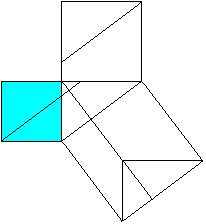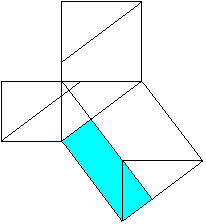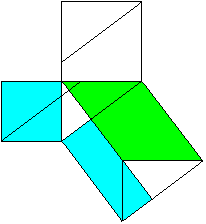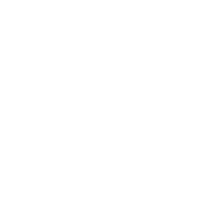a²+b²=c² Euklid's theorem (Euklid, ~300 BC) 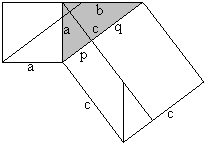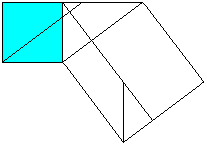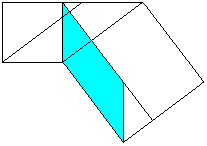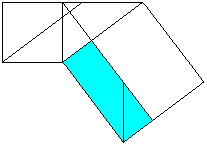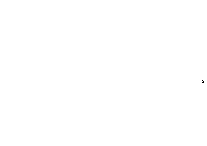a²=cp (You can show b²=cq in analogy.) Height formula 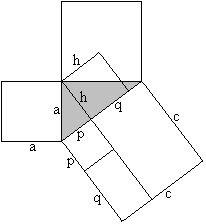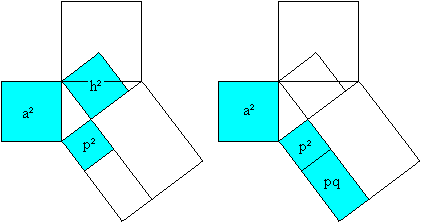a²=p²+h² (Pythagorean theorem), a²=pc=p²+pq (Euklid's theorem), hence h²=pq The Pythagorean theorem (Liu Hui, ~300, China) 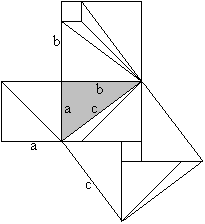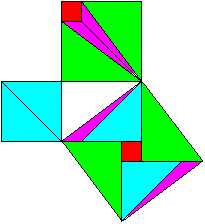a²+b²=c² The Pythagorean theorem ("The bride's chair", ~900, India) 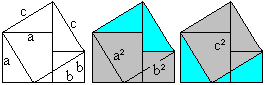a²+b²=c² The Pythagorean theorem (Atscharja Bhaskara, Indien,  ~1150) 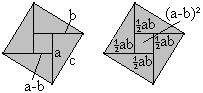c²=(a-b)²+2ab oder c²=a²+b² The Pythagorean theorem (Leonardo da Vinci, 1452-1519) 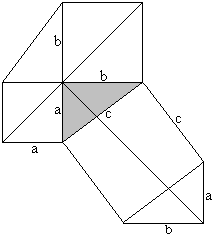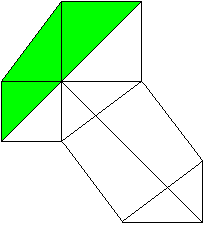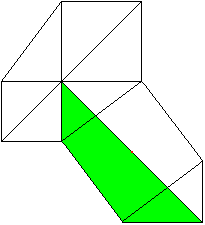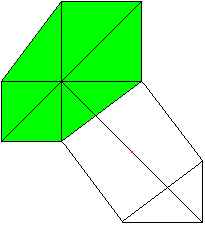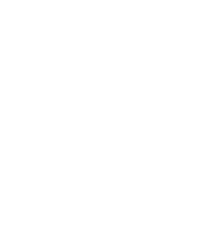a²+b²=c² The Pythagorean theorem (Arthur Schopenhauer's case was a=b, 1788-1860) 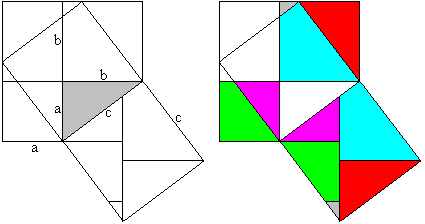a²+b²=c² The Pythagorean theorem (James Garfield 1876, later on the 20th US President) 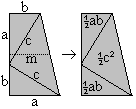You use the formula of the area of a trapezium [A=mh, here h=a+b and m=(a+b)/2] (a+b)²/2=c²/2+2*(1/2*ab) or a²+b²=c² The Pythagorean theorem (Hermann Baravalle 1945) 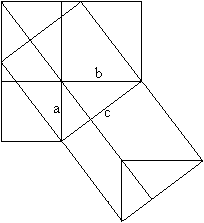......... 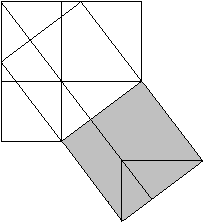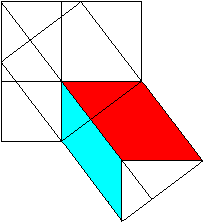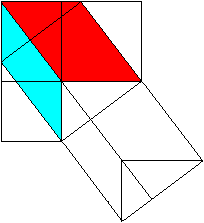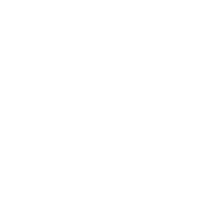c²=a²+b² The Pythagorean theorem 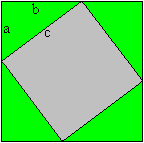(a+b)²=c²+4*(1/2ab) oder a²+b²=c² Cubes     top Cube of a sum (a+b)³=a³+3a²b+3ab²+b³ You can see both cubes and the six rectangular parallelepipeds in 3D-view: Cube of a difference The formula is (a-b)³=a³-3a²b+3ab²-b³. You convert it to (a-b)³=a³-3ab(a-b)-b³ for an illustration. ...... You take the drawing of the formula (a+b)³=a³+3a²b+3ab²+b³ from above and replace a by the difference a-b.  Then the edges are (a-b)+b with different combinations (on the left). The term (a-b)³ is illustrated by the blue cube (on the right). ...... 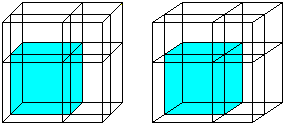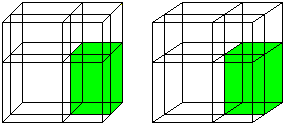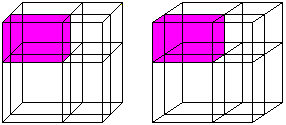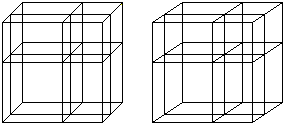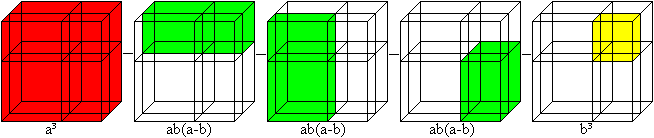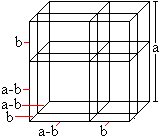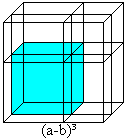You  recieve the blue cube, too, if you take away the three green bodies and the yellow cube from the red cube: (a-b)³ = a³-3ab(a-b)-b³ = a³-3a²b+3ab²-b³ https://orion.math.iastate.edu/dept/links/formulas/form1.pdf